2023年成考高起点每日一练《数学(文史)》9月13日专为备考2023年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

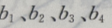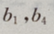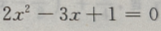1、已知成等差数列，且为方程的两个根，则的值为（）  

• A：
• B：
• C：
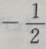
• D：

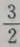
答 案：D

解 析：由根与系数的关系得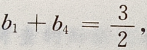由等差数列的性质得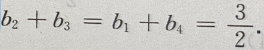

2、函数的图像与直线y=4的交点坐标为（）

• A：(0,4)
• B：(4,64)
• C：(1,4)
• D：(4,16)

答 案：C

解 析：令y=4^x=4，解得x=1，故所求交点为（1,4).

3、已知向量a=(3,4),b=(0,-2),则cos=()  

• A：
• B：
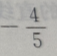
• C：
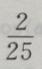
• D：

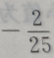
答 案：B

解 析：因为a=(3,4),b=(0,-2),  

4、直线2x-y+7=0,与圆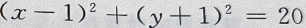的位置关系是（）  

• A：相离
• B：相交但不过圆心
• C：相切
• D：相交且过圆心

答 案：C

解 析：易知圆心坐标（1，-1），圆心到直线2x-y+7=0的距离d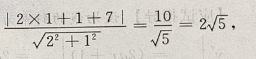 ∵圆的半径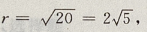 ∴d=r，∴直线与圆相切  

主观题

1、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.  

答 案：设每亩增种x棵,总收入味y元，则每亩种树(20+x)棵，由题意知增种x棵后每棵收入为（60-3x） 则有y=(90-3x)(20+x) 整理得y=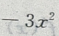+30x+1800 配方得y=+1875 当x=5时，y有最大值，所以每亩地最多种25棵

2、设函数f(x)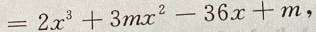且f'(-1)=-36 (Ⅰ)求m (Ⅱ)求f(x)的单调区间

答 案：(Ⅰ)由已知得f'=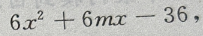 又由f'(-1)=-36得 6-6m-36=-36 故m=1. (Ⅱ)由(Ⅰ)得f'(x)=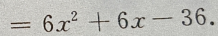 令f'(x)=0，解得 当x<-3时，f'(x)>0; 当-32时，f'(x)>0; 故f(x)的单调递减区间为(-3,2)，f(x)的单调递增区间为(-∞,-3),(2,+∞)  

3、设函数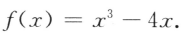
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．

答 案：(I）因为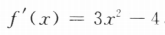，所以f'(2)=3×2²-4=8.(II）因为x＜-1，f(-1)=3.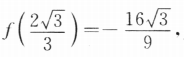f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为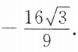

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

填空题

1、函数f(x)=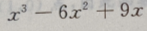在区间[-3,3]上的最大值为（）  

答 案：4

解 析：这题考的是高次函数的最值问题，可用导数来求函数在区间[-3,3]上的最值。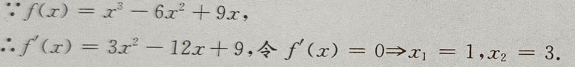 列出表格 由上表可知函数在[-3,3]上，在x=1点处有最大值为4.  

2、从某班的一次数学测试卷中任意抽出10份,其得分情况如下:81,98,43,75,60,55,78,84,90,70,则这次测验成绩的样本方差是（）  

答 案：252.84

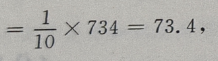
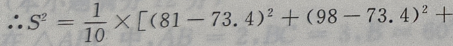
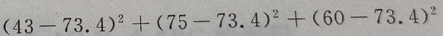
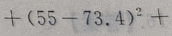
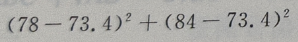
解 析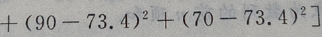： =252.84